
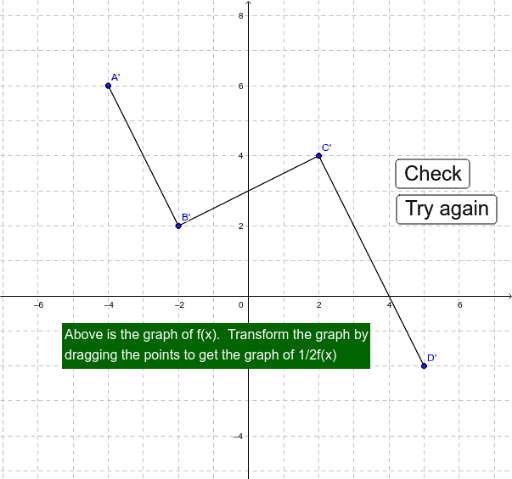
The x-coordinate of the point of intersection is displayed as 2.1661943. Describe how a horizontal stretch or compression affects a function, and express this type of transformation in function notation.

The graphs should intersect somewhere nearx=2.įor a better approximation, press then. For a window, use the values –3 to 3 for x and –5 to 55 fory.Press. horizontal asymptote 5.6 Rational Functions, 5.6 Rational Functions, 5.6 Rational Functions horizontal compression 3. 109, 115 rational function, from graph, 420 sine function, 267 sum-of-angle, 327 surface area cylinder, 73 transformation horizontal compression. A horizontal compression looks similar to a vertical stretch. To use a calculator to solve this, press and enter 1.2(5)x+2.8 next to Y1=. When b is greater than 1, a horizontal compression occurs.
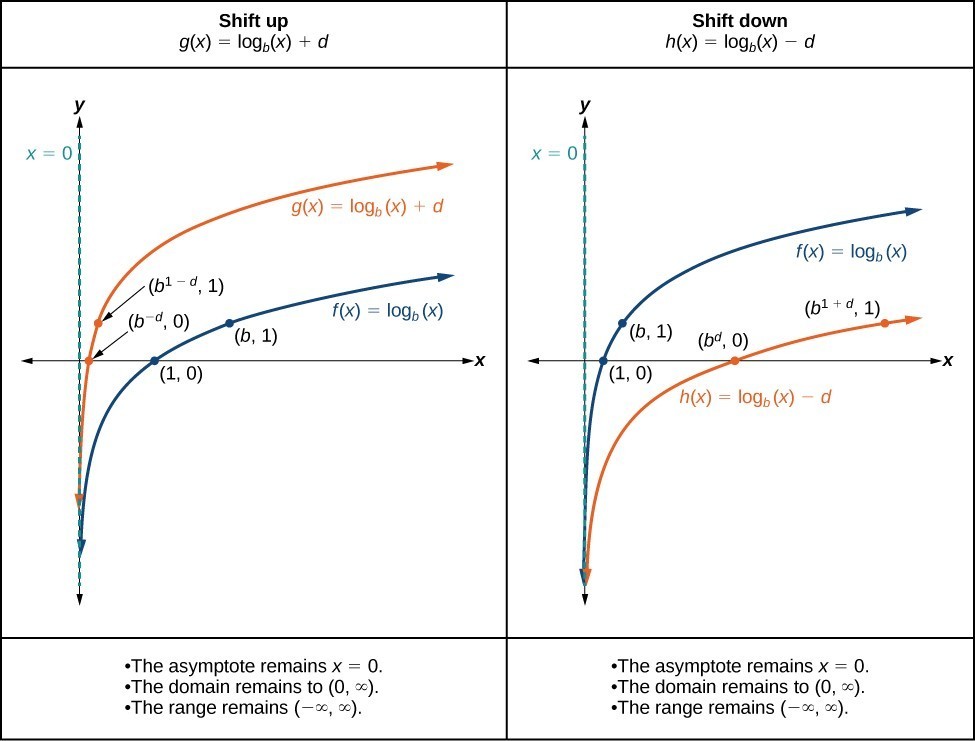
For example, the cube root of 8 is 2, because. If 0 < a < 1 0 < a < 1, then the graph will be compressed. Cube roots are pretty similar to square roots, except that their value is the number that, when multiplied by itself three times, is equal to the number under the radical, just as the square root of a number is the number that, when multiple by itself twice, is equal to the number under the radical. If a > 1 a > 1, then the graph will be stretched. Just as with other parent functions, we can apply the four types of transformations-shifts, reflections, stretches, and compressions-to the parent function f\left(x\right)= in the same window, the point(s) of intersection if any represent the solutions of the equation. Given a function f (x), f ( x), a new function g(x) af (x), g ( x) a f ( x), where a a is a constant, is a vertical stretch or vertical compression of the function f (x) f ( x). Transformations of exponential graphs behave similarly to those of other functions. Graph exponential functions shifted horizontally or vertically and write the associated equation.


 0 kommentar(er)
0 kommentar(er)
